Question

The median player salary for a professional football team was $457,200 in 2000 and $1,342,676 in 2008. Write a linear equation giving the median salary y in terms of the year x. (Let x = 0 represent 2000.)

Answer 1

The linear equation giving the median salary y in terms of the year x is:

y = 110,684.5x + 457,200

Explanation:

For calculating the linear equation first we need to calculate the slope of the equation represented with an m, the formula is the following:

`m=(y_(2)- y_(1)  )/(x_(2)-x_(1))`

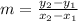
As in the problem it is said, x will represent the time so:

x1 will be the initial year so x1=2000

x2 will be the final year so x2=2008

Now the salary will be represented with the y so:

y1 will be the salary for the year 2000 then y1 = $457,200

y2 will be the salary for the year 2008 then y2 = $1,342,576

Then replacing the values in the equation we will have the following expresión:

`m=(1,342,676-457,200)/(2008-2000) = (885,476)/(8)=110,684.5`

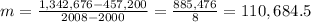
Now we have to replace this values in the following formula for linear equation

y-y1 = m(x-x1)

As they say that x represent 2000 as the initial year then when we replace we will have the following expresion

y - 457,200 = 110,684.5(x - 0)

y = 110,684.5x + 457,200

To verify our equation we can check for the salary in 2008 as it is 8 years after of 2000 x=8 then

y = 110,684.5 (8) + 457,200

y = 885,476 + 457,200 = 1,342,676