Question

Which equation shows a slope of -5 and a y-intercept of (0,1) ?

y = -1x - 5

y = -5x + 1

y = 1x - 5

y = 5x = 1

Answer 1

The equation that represents a slope of -5 and y-intercept of (0,1) is:

`f(x) = -5x + 1`

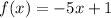
Explanation:

The equation of a line can be described by a first order equation in the following format:

`f(x) = ax + b`

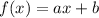
In which a is the slope of the line and b is the y-intercept.

Solution:

The problem states that the slope is -5, so:

`a = -5`

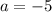
y intercept is (0,1), so

`b = 1`

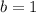
The equation that represents a slope of -5 and y-intercept of (0,1) is:

`f(x) = -5x + 1`

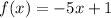
Why the others are wrong?

`y = -1x - 5`

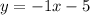
Here, the slope is -1, and the y-intercept is (0,-5).

`y = 1x-5`

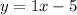
For this option, the slope is 1 and the y-intercept is (0,-5).

`y = 5x - 1`

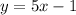
Is it 5x - 1? If so, the slope is 5, and the y-intercept is (0,-1).