Question

If the net flux through a Gaussian surface is zero, the following four statements could be true. Which of the statements must be true? There are no charges inside the surface. The net charge inside the surface is zero. The electric field is zero everywhere on the surface. The number of electric field lines entering the surface equals the number leaving the surface.

Answer 1

The net flux through a Gaussian surface being zero must mean that the net charge inside the surface is zero. It indicates an equal number of electric field lines entering and exiting the surface, which is a consequence of Gauss's Law.

Step-by-step explanation:

If the net flux through a Gaussian surface is zero, this could mean several things. However, one statement that must be true is that the net charge inside the surface is zero. This is a direct consequence of Gauss's Law, which relates the electric flux through a closed surface to the charge enclosed within it. If the flux is zero, it indicates that there is no net charge within the surface. This does not necessarily mean there are no charges inside the surface; they could be present but sum up to zero.

Moreover, the net flux being zero does not guarantee that the electric field is zero everywhere on the surface. What must be true is that the number of electric field lines entering the surface equals the number leaving the surface, ensuring that the net flux is zero.

In summary, the fact that the net flux through a Gaussian surface is zero does not mean there are no charges within it, nor does it mean the electric field is zero on the surface. The essential truth is that the net charge enclosed is zero, correlating with an equal number of electric field lines entering and leaving the Gaussian surface.

Answer 2

The statements which are true are as follows:

1. The net charge inside the surface is zero.
2. The electric field is zero everywhere on the surface.
3. The number of electric field lines entering the surface equals the number leaving the surface.

Step-by-step explanation:

The electric flux through a surface is defined as the number of electric field lines passing through the unit area of that surface normally.

It is given as

`\phi = \vec E \cdot \vec A\ \ \ \ \ ...........\ (1).`

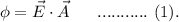
According to Gauss' law, it is given as

`\phi=(q)/(\epsilon_o)\ \ \ \ .........\ (2).`

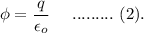
where,

`q` is the net charge enclosed by the surface.

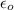`\epsilon_o` is the electrical permittivity of free space.

Statement 1: There are no charges inside the surface.

It is not a necessary condition for electric flux through that surface to be zero because the even if there is some charge present inside the surface such that the net charge(sum of all charges) inside the surface is zero, then the electric flux through that surface is also zero.

Thus, this statement need not to be necessarily true.

Statement 2: The net charge inside the surface is zero.

As mentioned in the above part of the answer, if the net charge inside the surface is zero then the electric flux through that surface must be zero.

Thus, this statement must be true.

Statement 3: The electric field is zero everywhere on the surface.

According to the equation (1), the electric flux through that surface must be zero.

Thus, this statement must be true.

Statement 4: The number of electric field lines entering the surface equals the number leaving the surface.

If the number of electric field lines passing through that surface is equal to that of electric field lines leaving that surface then it means there is not any charge present inside the surface. In that case, the electric flux through the surface is zero.

Thus, this statement must be true.