Answer:
(d) 5.56%
Explanation:
In the question,
The amount David can take in lump sum = $10 million
or,
The amount he can receive for 25 years = $750,000/ year
Now,
If David need to take break after taking the lump sum amount is given by,
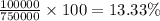
Now,
From the Annuity table we can find out the value for the percent 13.33% for the time period of 25 years.
That is lying in between 5 and 6 tending towards 6 more.
So,
From the given options we can see that,
Rate of return can be = 5.56%
If the payment is made at the end of the year then only we can say that the rate of return is 5.56%.
Therefore, the correct option is (d).