Question

A ball rolls across a floor with an acceleration of 0.100 m/s2 in a direction opposite to its velocity. The ball has a velocity of 4.00 m/s after rolling a distance 6.00 m across the floor. What was the initial speed of the ball?

Answer 1

4.15 m/s

Step-by-step explanation:

Its given that acceleration is 0.1 m/s² with a direction opposite to the velocity. Since, the direction of acceleration is opposite to the velocity, this gives us a hint that the velocity is decreasing and so acceleration would be negative.

i.e.

acceleration = a = - 0.1 m/s²

Distance covered = S = 6m

Velocity after covering 6 meters = Final velocity =
`v_(f)` = 4 m/s

We need to find the initial speed, which will be the same as the magnitude of initial velocity.

Initial velocity =
`v_(i)` = ?

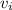3rd equation of motion relates the acceleration, distance, final velocity and initial velocity as:

`2aS = (v_(f))^(2)-(v_(i))^(2)`

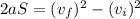
Using the known values in the formula, we get:

`2(-0.1)(6)=(4)^(2)- (v_(i))^(2)\\\\ (v_(i))^(2)=16+1.2\\\\ (v_(i))^(2)=17.2\\\\ v_(i)=4.15`

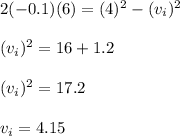
Thus, the initial speed of the ball was 4.15 m/s