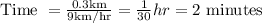Question

Duplain St. is 300 m long and runs from west to east between Baron and Burkey. If Keith is strolling east from Baron at an average velocity of 3 km/hr, and Sue is power-walking west from Burkey at an average velocity of 6 km/hr, how long will it take them to meet?

Question 13 options:

1 minute

2 minutes

3 minutes

6 minutes

Answer 1

2 minutes

Step-by-step explanation:

Answer 2

Sue from Burkey and Keith from Baron will meet in 2 minutes

Answer: Option b

Step-by-step explanation:

Time taken can be calculated when distance and the speeds are given. Here speeds of Keith and Sue are given. So, we have to find the relative speeds in order to calculate the time taken.

When two objects travel in same direction the relative speed will be the difference between speeds. Similarly when two objects travel in opposite direction, the relative speed will be the sum of given speeds.

Given:

Speed of Sue from Burkey is 6 km/hr and speed of Keith from Baron is 3 km/hr.

The distance between Burkey and Baron is 300 m.

From the formula,
`d=s * t`

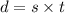
where d is distance,s is speed and t is time

It can be derived that,
`t=(d)/(s)`

s = sum of given speeds = 3 km/hr + 6 km/hr = 9 km/hr

d = 300 m = 0.3 km
`\text {Time }=\frac{0.3 \mathrm{km}}{9 \mathrm{km} / \mathrm{hr}}=(1)/(30) h r=2 \text { minutes }`