Question

Which ordered pairs are in the solution set of the system of linear inequalities?

y > Negative one-halfx

y < One-halfx + 1

On a coordinate plane, 2 straight lines are shown. The first solid line has a negative slope and goes through (0, 0) and (4, negative 2). Everything above the line is shaded. The second dashed line has a positive slope and goes through (negative 2, 0) and (2, 2). Everything below the line is shaded.
(5, –2), (3, 1), (–4, 2)
(5, –2), (3, –1), (4, –3)
(5, –2), (3, 1), (4, 2)
(5, –2), (–3, 1), (4, 2)

Answer 1

Its C

Explanation:

I just got 100% on the Quiz

Answer 2

The ordered pairs (5 , -2) , (3 , 1) , (4 , 2) are in the set of the solution ⇒

3rd answer

Explanation:

- The first line has negative slope and passing through points (0 , 0)

and (4 , -2)

∵
`y>(-1)/(2)x`

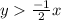
- The second line has positive slope and passing through points (-2 , 0)

and (2 , 2)

∵
`y<(1)/(2)x+1`

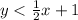
- Look to the attached figure to see the common part of the solutions

- The red shaded represents the inequality
`y>(-1)/(2)x`

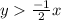
- The blue shaded represents the inequality
`y<(1)/(2)x+1`

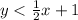
- The shaded part with two colors represents the common solutions

of the two inequalities

- Lets find the ordered pairs which are in the solution set of the system

of linear inequalities

- Points (-4 , 2) , (-3 , 1) , (4 , -3) lies out the common shaded

- Points (5 , -2) , (3 , 1) , (3 , -1) , (4 , 2)

∵ Point (5 , -2) lies in the common shaded part

∵ Point (3 , 1) lies in the common shaded part

∵ Point (4 , 2) lies in the common shaded part

∴ The ordered pairs (5 , -2) , (3 , 1) , (4 , 2) are in the set of the

solution