Answer:
 and
and

Step-by-step explanation:
To solve this problem, we need to use the following formula
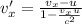
Givens:
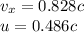
In same direction, we have
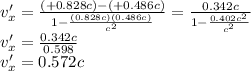
Notice, that we just replaced each given value, and solve basic operations.
In different direction,
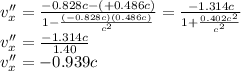
As you can observe, to solve this kind of problem, you just neet to consider the right sign of each velocity, when they are in the same direction, they must have the same sign, but when they are in opposite direction, they must have different signs.
Therefore, the answers are
 and
and
