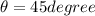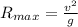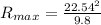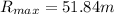Question

You buy a plastic dart gun, and being a clever physics student you decide to do a quick calculation to find its maximum horizontal range. You shoot the gun straight up, and it takes 4.6 s for the dart to land back at the barrel.

Answer 1

`R_(max) = 51.84 m`

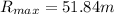
Step-by-step explanation:

When we shoot the dart upwards the time taken by the dart to go straight up and again come back is given as

`t = 4.6 s`

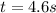
here we can say

`\Delta y = 0 = v_i t + (1)/(2)at^2`

`0 = v_i t - (1)/(2)(9.8)t^2`

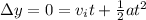
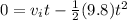
put t = 4.6 s then we have

`v_i = 22.54 s`

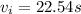
Now in order to find the maximum range we can say

`R = (v^2 sin2\theta)/(g)`

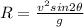
so in order to have maximum range we can say

`\theta = 45 degree`

`R_(max) = (v^2)/(g)`

`R_(max) = (22.54^2)/(9.8)`

`R_(max) = 51.84 m`