Question

An airplane is flying with a velocity of 248 m/s at an angle of 30.0° with the horizontal, as the drawing shows. When the altitude of the plane is 2.5 km, a flare is released from the plane. The flare hits the target on the ground. What is the angle θ?

Answer 1

49.55° degrees below horizontal

Step-by-step explanation:

Hi

We have the initial velocity of the flare is 248 m/s at 30° below horizontal and considering the gravity as 9.8m/s^2

We calculate the time it takes to reach the ground using the next equation and the next steps

`h=vo*t*sin(30)+0.5gt^2`

`2500 = 248*t*0.5+4.9t^2`

`2500 = 124*t+4.9t^2`

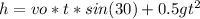
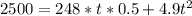
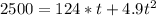
From the second grade equation we obtain two results, the negative one is dismiss, so we obtain that time is equal to 13.2372

Now we have to calculate the vertical speed just before it hits the ground, we have to separate the velocity in vectors Vx (horizontal) and Vy (vertical)

Vy = Vo*sin(30)+gt = 124+9.8*13.05 = 251.89

Vx= Vo*cos(30)=214.77

Now we use the next equation for the angle

Θ
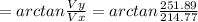`= arctan(Vy)/(Vx)  = arctan(251.89)/(214.77)`= 49.55° degrees