Answer: 24.77 m/s
Explanation: Knowing the following:
Initial Velocity (Vo) = 13.6 m/s
Gravity (g) = 9.8
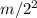
total distance = 21.9m
To know the final velocity (Vf) on which the ball drops the ground, we can just sum the initial velocity (Vo) plus the velocity gained through the gravity:
Vf = Vo + g*t
However, we dont know the time the takes to touch the ground. But we can get it using the following.
D = Vo * t0 + (
 * g *
* g *
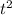 )
)
This is a cuadratic equation that can be solved in several ways. But first, we need to acomadate this equation
21.9 = 13.6 * t + 4.9*
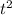
4.9
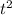 + 13.6 * t -21.9 = 0
+ 13.6 * t -21.9 = 0
On quadratic equation, we can know the value for time (t) by running the following equation:
±
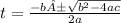
Where:
a = 4.9
b = 13.6
c= -21.9
Running this equation we get the following values:
t = 1.14 ;−3.91
We take the positive time, because time runs only one way. With this time we do the equation:
Vf = Vo + g*t
Which give us:
Vf = 13.6 + 9.8 * 1.14
Vf= 24.77 m/s