Answer:
0.122 radians
Step-by-step explanation:
Given that the muzzle speed is,
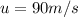
And the distance of the object is,
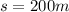
And acceleration due to gravity is
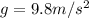
Therefore negative acceleration due to gravity for upward motion.
Now,
The x component of velocity will be,

The y component of velocity will be,
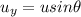
And the horizontal displacement is given. Now horizontal displacement is,
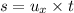
Here,
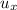 is horizontal velocity and t is time.
is horizontal velocity and t is time.
Substitute all the values in above equation, we get
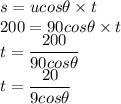
Now, in y direction we can calculate displacement and in y direction displacement is zero.
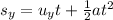
Substitute all the variables.

Therefore the required angle of elevation is 0.122 radians.