Answer:
a)
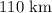
b)
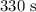
Step-by-step explanation:
Given:
- Acceleration of the rocket,
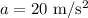
- Time taken ,
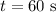
Equations of motion will be used to solve get maximum altitude and total time taken
Distance travelled by the rocket during acceleration
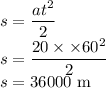
Let v be the velocity of the rocket at the end of 60 s which is given by
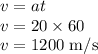
a) Now the rocket will be under the gravity after its fuel ends, at the highest point of trajectory its final velocity will be zero
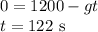
During this time the rocket will rise to the maximum height under gravity
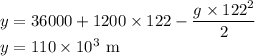
Hence the maximum height of the rocket is calculated.
b) When the rocket falls back to the ground its displacement will be zero with respect to the ground
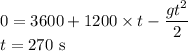
The total time
