Answer:
a) We need 32.65 W of power to maintain the temperature at 197°C.
b) The range of wattage allowed is (32.53W, 32.76W)
Step-by-step explanation:
a) In order to find the needed wattage to maintain a temperature of 197°C for the crystals, we need to start by substituting that value into the provided function:
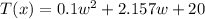
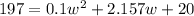
and set the equation equal to zero by subtracting 197 from both sides, so we get:
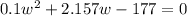
To accurately solve this equation we can make use of the quadratic formula, which in this case will be:
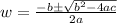
in this case:
a=0.1
b=2.157
c=-177
(which come from the original equation according to their position in the equation with the form
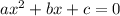
so we can substitute them into the formula like this:
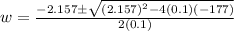
We can solve this formula by directly plugging it into the calculator. That way you will get an exact answer. If you have troubles inputing this into the calculator, you can follow order of operations to solve it (parenthesis, exponentials, multiplication and division, addition and subtraction) but use as many decimal numbers as you can in the middle operations so you get a precise answer.
When inputing it into the calculator we get two answer:
w= -54.22W and w=32.65W
we use the positive answer, since that means that the power is being inputed into the system, a negative answer would mean you are retrieving power from the system which would cool the system down.
So we need 32.65W of power to maintain the temperature at 197°C
b) We need to follow the same procedure to find the answer for b. The only change is that the temperature may vary from 196°C to 198°C (197±1)°C
so the equations to solve change to:
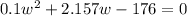 for 196°C
for 196°C
(in this case the "c" on the quadratic formula changes to -176)
when solving this equation we get an answer of:
w=32.53W
and
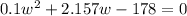 for 198°C
for 198°C
(in this case the "c" in the quadratic formula changes to -178)
when solving this equation we get an answer of:
w=32.76W
so the powers must be between 32.53W and 32.76W for the temperature to stay in an acceptable range.