Answer:
6.02 s
Step-by-step explanation:
We can write the position of the stock car as:
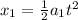
where
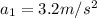 is the acceleration of the stock car.
is the acceleration of the stock car.
The sport car instead starts its motion only 1.3 s afterwards, therefore its position at time t can be written as

where
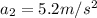 is the acceleration of the sport car
is the acceleration of the sport car
(we can verify indeed that when t = 1.3 s,
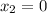 ).
).
The sport car reaches the stock car when the two positions are equal:
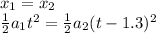
Rewriting the equation,
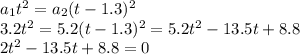
This is a second-order equation with two solutions:
t = 0.73 s
t = 6.02 s
We discard the first solution since we are only interested in the times > 1.3 s, therefore the sport car overcomes the stock car after
6.02 seconds.