Answer:
72,300 years.
Step-by-step explanation:
- Initial mass of this sample: 504 grams;
- Current mass of this sample: 63 grams.
What's the ratio between the current and the initial mass of this sample? In other words, what fraction of the initial sample hasn't yet decayed?
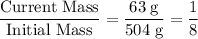 .
.
The value of this fraction starts at 1 decreases to 1/2 of its initial value after every half-life. How many times shall 1/2 be multiplied to 1 before reaching 1/8?
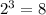 . It takes three half-lives or
. It takes three half-lives or
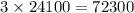 years to reach that value.
years to reach that value.
In certain questions the denominator of the fraction is large. It might not even be an integer power of 2. The base-x logarithm function on calculators could help. Evaluate
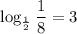 to find the number of half-lives required. In case the base-x logarithm function isn't available, but the natural logarithm function
to find the number of half-lives required. In case the base-x logarithm function isn't available, but the natural logarithm function
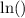 is, apply the following expression (derived from the base-changing formula) to get the same result:
is, apply the following expression (derived from the base-changing formula) to get the same result:
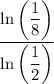 .
.