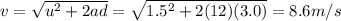Question

A dog walking to the right at 1.5\,\dfrac{\text m}{\text s}1.5sm​1, point, 5, space, start fraction, m, divided by, s, end fraction spies a cat ahead, and begins chasing the cat with a constant acceleration of 12\,\dfrac{\text m}{\text s^2}12s2m​12, space, start fraction, m, divided by, s, start superscript, 2, end superscript, end fraction.

What is the velocity of the dog after running for 3.0\,\text m3.0m3, point, 0, space, m?

​

Answer 1

8.6 m/s

Step-by-step explanation:

We can find the final velocity of the dog by using the following SUVAT equation:

`v^2-u^2=2ad`

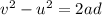
where

u is the initial velocity

a is the acceleration

d is the distance covered

For the dog in the problem, we have

u = 1.5 m/s

`a = 12 m/s^2`

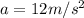
And the distance covered is

d = 3.0 m

Therefore, we can re-arrange the equation to find the final velocity, v:

`v=√(u^2+2ad)=√(1.5^2+2(12)(3.0))=8.6 m/s`