Question

To take off from the ground, an airplane must reach a sufficiently high speed. The velocity required for the takeoff, the takeoff velocity, depends on several factors, including the weight of the aircraft and the wind velocity.

Part A A plane accelerates from rest at a constant rate of 5.00 m/s2 along a runway that is 1800 m long. Assume that the plane reaches the required takeoff velocity at the end of the runway. What is the time tTO needed to take off? Express your answer in seconds using three significant figures. View Available Hint(s) tTO t T O = s That's not quite right. Please check your formatting and try again. No credit lost. Try again. Previous Answers
Part B Complete previous part(s) Part C What is the distance dfirst traveled by the plane in the first second of its run? Express your answer numerically in meters using three significant figures. View Available Hint(s) dfirst d f i r s t d_first = nothing m Part D What is the distance dlast traveled by the plane in the last second before taking off? Express your answer numerically in meters using three significant figures. View Available Hint(s) dlast d l a s t d_last = nothing m

Answer 1

A-B) 26.8 s

The plane accelerates at a rate of

`a=5.00 m/s^2`

And the total distance covered by the plane is the length of the runaway

d = 1800 m

The plane starts from rest, so its initial velocity is

u = 0 m/s

We can solve this part of the problem by using the following SUVAT equation:

`d=ut+ (1)/(2)at^2`

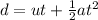
where

t is the time the plane needs to cover the distance d.

Since u = 0, the equation can be rewritten as

`d=(1)/(2)at^2`

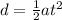
So we can now solve for t:

`t=\sqrt{(2d)/(a)}=\sqrt{(2(1800))/(5.00)}=26.8 s`

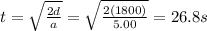
C) 2.50 m

We now want to calculate the distance travelled by the plane in the first second of its motion: therefore, we just need to use

t = 1 s

And use again the same equation

`d=ut+ (1)/(2)at^2`

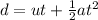
Again, since u = 0 at the beginning of the motion,

`d=(1)/(2)at^2`

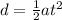
So by substituting t = 1 we find

`d=(1)/(2)(5.00)(1^2)=2.50 m`

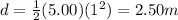
D) 132 m

This part is a bit different, since first we have to find the velocity of the plane when the last second starts.

As we found in part A-B, the total time of the motion is 26.8 s. So we need to find the velocity of the plane when the last second starts, which means at

`t' = 26.8-1=25.8 s`

The velocity is given by

`u' = u+at'`

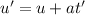
where

u = 0

a = 5.00 m/s^2

t' = 25.8 s

Substituting,

`u' = 0 +(5.00)(25.8)=129 m/s`

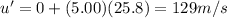
Now we can use the following SUVAT equation:

`d=u' \Delta t + (1)/(2)a\Delta t^2`

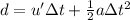
where

`u' = 129 m/s`

`\Delta t = 1s`

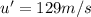
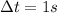
to find the distance covered by the plane in the last second. Substituting,

`d=(129)(1) + (1)/(2)(5.00)(1)^2=132 m`