Answer:
Minimum number of lines, N = 3690.64
Step-by-step explanation:
Mean of wavelengths,
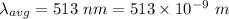
Smallest resolvable wavelength difference,

Resolution of diffraction grating is given by :
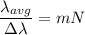
For first order, m = 1
N is the minimum number of lines
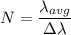
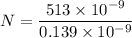
N = 3690.64
Hence, the minimum number of lines needed in a diffraction grating that can resolve these lines in the first order is 3690.64. Hence, this is required solution.