Question

A company has a policy of retiring company cars; this policy looks at number of miles driven, purpose of trips, style of car and other features. The distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of 46 months and a standard deviation of 5 months. Using the 68-95-99.7 rule, what is the approximate percentage of cars that remain in service between 51 and 56 months?

Answer 1

Answer: 13.5%

Explanation:

Given : The distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of
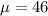`\mu=46` months and a standard deviation of
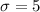`\sigma=5`months.

To find : The approximate percentage of cars that remain in service between 51 and 56 months.

We can see that
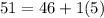`51=46+1(5)` i.e. 51 is one standard deviation to the right from the mean. (1)

And
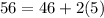`56=46+2(5)` i.e. 56 is two deviations two the right from the mean. (2)

According to the 68-95-99.7 rule, 95% of the population falls within two deviation from the mean (Both in left and right).

But given situation only happens in right side of the normal curve.

For that we first find half area for two deviation right from the mean (for x<56) .

i.e. Area under the curve that is 2 standard deviations from the mean =
`(95\%)/(2)=47.5\%`

Also by considering (2), we need area between one standard deviation and the two standard deviation.

According to the 68-95-99.7 rule, 68% of the population falls within one deviation from the mean (Both in left and right).

Then for (1), Area under the curve that is one standard deviation from the mean =
`(68\%)/(2)=34\%`

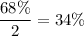
So, the required area will be : 47.5%-34%=13.5%

Hence, the approximate percentage of cars that remain in service between 51 and 56 months = 13.5%