Answer:
The answer is 91
Explanation:
We have the following equality:

Then a must satisfy that
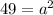 . So,
. So,
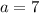 or
or
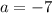 .
.
1) If a=7, then, it follows for the first equality that 56=14b. Then b=4. Finally, substituting b=4 in the first equality we obtain that -64=16-c. So, c= 80. We conclude that
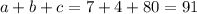 .
.
As the problem states, we only consider values of a greater than zero. Then 91 is the only solution for
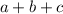 .
.