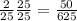Question

A telephone number contains 10 digits, including a 3-digit area code. Bob remembers the area code and the next 5 digits of the number. He also remembers that the remaining digits are not 0, 1, 2, 5, or 7. If Bob tries to find the number by guessing the remaining digits at random, the probability that he will be able to find the correct number in at most 2 attempts is closest to which of the following?

A. 1/625
B. 2/625
C. 4/625
D. 25/625
E. 50/625

Answer 1

C. 50/625

Explanation:

We just need to know how much posibities we have for the last two numbers. Then as the number are not 0, 1, 2, 5 of 7 it have to be 3, 4, 6, 8, or 9. We have 5 options for the nineth number and 5 for the tenth, becase the numbers could be repeated. Multiplying the options for each number we have 25 and the we have two opportunities then the probability is:

`(2)/(25)`

This fraction is the same as
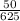`(50)/(625)` because:

`(2)/(25)(25)/(25)=(50)/(625)`