Question

Suppose a bank charges a base rate of $5 plus $0.10 per check for your checking account. You can switch to a different account that charges $4 plus $0.20 per check. For what number of checks is the monthly cost of the two accounts the same? What is the cost?

Answer 1

10 number of checks.

Cost = $6

Explanation:

Given that:

Fixed Charges of first bank = $5

Charges of first bank per check = $0.10

Fixed Charges of second bank = $4

Charges of second bank per check = $0.20

To find:

Number of checks such that the charges for the banks become the same?

Solution:

Let the number of checks =
`x`

Cost for the first bank for
`x` checks = $5 + $0.10
`x`

Cost for the second bank for
`x` checks = $4 + $0.20
`x`

As per question statement, both the costs are the same.

Comparing the values:

`5 + 0.10x = 4 + 0.20x\\\Rightarrow 0.10x = 1\\\Rightarrow x = 10`

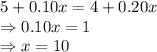
So, for 10 number of checks the cost will be same.

The cost = 4 + 0.20
`*` 10 = $6