Question

A spy is trying to escape. She must get by four guards. Each guard takes half of her remaining money. She then $64 for her plane ticket. How much money does she have to start with in order to make her escape?

Answer 1

The spy must have at the start the amount of $1,024 in order to escape

Explanation:

Let

a ------> amount of money that the spy must have at the start to escape

y ----> the remaining money

x ----> the number of guards

In this problem the remaining money is going to be reduced by half, every time the spy passes through a guard, so we can use an exponential function of the form

`y=a(b^(x))`

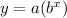
where

a is the initial value (amount of money at the start)

b is the base

b=(1-r)

r is the rate of decay

In this problem we have

r=50% -----> r=0.50

The value of b is

b=(1-0.50)=0.50

substitute

`y=a(0.50^(x))`

we know that

In order to escape after the fourth guard the amount of money remaining must be equal to $64

so

For x=4, y=$64

substitute in the equation and solve for a

`64=a(0.50^(4))`

`64=a(0.0625)`

`a=64/(0.0625)`

`a=\$1,024`

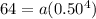
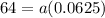
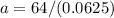
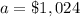
therefore

The spy must have at the start the amount of $1,024 in order to escape