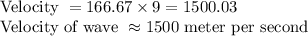Question

If a wave has a wavelength of 9 M and a period Of 0.006 what is the velocity of the wave​

Answer 1

X=9m
T=0.006
V= 1/T
V= 9m/0.006 V=1500 m/s
Or simply 9/0.006=1500

Answer 2

The velocity of wave having wavelength of 9 meter and time period 0.006 is 1500 meter per second.

Solution:

By using the velocity wavelength frequency relationship, velocity is the product of frequency and wavelength

`\text {Velocity }(v)=\text {Frequency}(f) * \text {Wavelength}(\lambda)-----(1)`

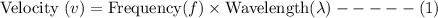
Frequency is the inverse of time period.

`\begin{array}{l}{\text { Frequency }=\frac{1}{\text { Time period }}} \\\\ {\text { Time period }=0.006} \\\\ {\text { Frequency }=(1)/(0.006)=166.666} \\\\ {\text { Frequency } \approx 166.67 \mathrm{Hz}}\end{array}`

Wavelength = 9 meter

Apply the frequency and wavelength value in equation 1, we get,

`\begin{array}{l}{\text { Velocity }=166.67 * 9=1500.03} \\ {\text { Velocity of wave } \approx 1500 \text { meter per second }}\end{array}`