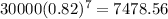Question

40 PTS! EXPONENTIAL FUNCTIONS!

Some years ago, Mr. Smith & Mr Jones bought a car on the same day. The value of both cars has decreased every year.

Mr Smith: Function f can be used to determine the value of Mr. Smith's car:
f(x) = 23, 000b ˣ
Where x is the time elapsed, in years since the car was bought
& y the value of Mr. Smith's car.

Mr. Jones: Function g can be used to determine the value of Mr. Jones' car:
g(x) = a(0.82) ˣ
Where x is the time elapsed in years since the car was bought
& y the value of Mr. Jones' car.

Two years after Mr. Smith bought his car, it was valued at $14, 720.
Three years after Mr. Jones bought his car, it was valued at $16, 541. 04.
Today, the value of Mr Smith's car is $4,823.45.
What is the value of Mr Jones' car today?

Answer 1

Jones' car is worth $7478.56 now

Explanation:

Mr Smith:
`f(x)=23000*b^x`

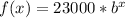
Mr Jones:
`g(x) = a(0.82)^x`

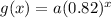
After two years, Mr. Smith's car is $14,720

We can use this to solve for b in his equation.

`23000b^2=14720\\b^2=(16)/(25)\\√(b^2)=\sqrt{(16)/(25)} \\b = (4)/(5)`

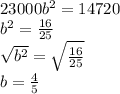
Mr Smith:
`f(x) = 23000((4)/(5))^x`

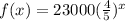
Then, we can use the value of Mr. Smith's car today to find the amount of time has passed.

`23000((4)/(5))^x =4823.45\\(4)/(5)^x=0.20971\\ ln(0.8^x)=ln(0.20971)\\ xln(0.8)=ln(0.20971)\\x=(ln(0.20971))/(ln(0.8)) = 7`

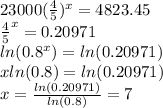
For the final price, 7 years has passed.

We can use Jones' info to find his equation

`a(0.82)^3=16541.04\\a(0.5513)=16541.04\\a=(16541.04)/(0.5513) \\a = 30000`

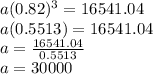
Jones:
`g(x) = 30000(0.82)^x`

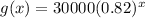
Now we just plug in x = 7 to find our value

`30000(0.82)^7=7478.56`