Question

the graph of a line in the xy-plane has slope of 7 and contains the point(6,28). A second line passes through the points (3,7) and (-1,-13). These lines intersect at point (x,y). What is the value of x?

Answer 1

x = 3

Explanation:

We require the equations of the 2 lines.

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

The line has slope = 7, hence

y = 7x + c ← is the partial equation

To find c substitute (6, 28) into the partial equation

28 = 42 + c ⇒ c = 28 - 42 = - 14

y = 7x - 14 → (1)

Calculate the slope of the second line using the slope formula

m = (y₂ - y₁ ) / (x₂ - x₁ )

with (x₁, y₁ ) = (3, 7) and (x₂, y₂ ) = (- 1, - 13)

m =
`(-13-7)/(- 1-3)` =
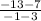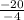`(-20)/(-4)` = 5, thus

y = 5x + c ← is the partial equation

To find c substitute either of the 2 points into the partial equation

Using (3, 7), then

7 = 15 + c ⇒ c = 7 - 15 = - 8

y = 5x - 8 → (2)

Solving (1) and (2) by equating the right sides

7x - 14 = 5x - 8 ( subtract 5x from both sides )

2x - 14 = - 8 ( add 14 to both sides )

2x = 6 ( divide both sides by 2 )

x = 3

The x- coordinate of the point of intersection is x = 3