Question

Determine if the graph shows two quantities that vary directly. If possible, determine the constant of proportionality. Explain your reasoning.

Answer 1

Do not vary directly.

Explanation:

A proportional relation between two variables x and y can be expressed as:

y = kx

where, k is the constant of proportionality.

The above equation can be rewritten as:

`k=(y)/(x)`

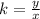
This equation should hold true for all the values of x and y that are applicable in the given scenario. This means, if x and y vary directly, the ratio of y to x must be a constant for all the values of y and x.

From the given graph, we can see the following points:

(0.3, 200) , (0.9, 400), (1.5, 600)

For the first point (0.3, 200):

`k=(200)/(0.3)=666.67`

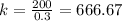
For the second point (0.9, 400):

`k=(400)/(0.9)=444.44`

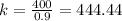
For the third point (1.5, 600):

`k=(600)/(1.5)=400`

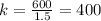
From here we can see that the ratio of y to x is not a constant. This means, the two quantities shown in the graph do not vary directly. There is only a linear relationship between the lines, not a proportional relationship