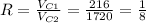Question

What is the ratio of the volume of a cube with edge length six inches to the volume of a cube with edge length one foot? Express your answer as a common fraction.

Answer 1

The ratio is
`(1)/(8)`

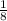
Explanation:

The volume of a cube with edge length a is:

`V = a^(3)`

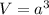
We have two cubes:

Cube 1: The one with edge length of six inches.

Cubs 2: The one with edge length of one foot.

The ratio is:

`R = (V_(C1))/(V_(C2))`

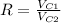
In which
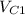`V_(C1)` is the volume of the first cube and
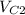`V_(C2)` is the volume of the second cube.

Volume of the first cube

The edge length is 6 inches, so
`a = 6`.

`V_(C1) = 6^(3) = 216 inches^(3)`

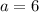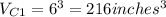
Volume of the second cube

To express the ratio as a common fraction, both volumes must be in the same unit. So we must pass the edge length of the second cube to inches.

The second cube has edge length of one foot. Each foot has twelve inches. So

`V_(C2) = 12^(3) = 1720 inches^(3)`

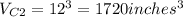
Ratio:

`R = (V_(C1))/(V_(C2)) = (216)/(1720) = (1)/(8)`