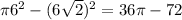Since you mentioned calculus, perhaps you're supposed to find the area by integration.
The square is circumscribed by a circle of radius 6, so its diagonal (equal to the diameter) has length 12. The lengths of a square's side and its diagonal occur in a ratio of 1 to sqrt(2), so the square has side length 6sqrt(2). This means its sides occur on the lines
 and
and
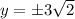 .
.
Let
 be the region bounded by the line
be the region bounded by the line
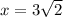 and the circle
and the circle
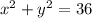 (the rightmost blue region). The right side of the circle can be expressed in terms of
(the rightmost blue region). The right side of the circle can be expressed in terms of
 as a function of
as a function of
 :
:
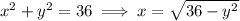
Then the area of this circular segment is
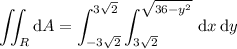
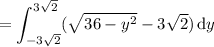
Substitute
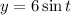 , so that
, so that
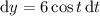
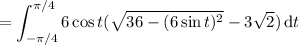
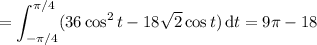
Then the area of the entire blue region is 4 times this, a total of
 .
.
Alternatively, you can compute the area of
 in polar coordinates. The line
in polar coordinates. The line
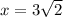 becomes
becomes
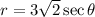 , while the circle is given by
, while the circle is given by
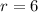 . The two curves intersect at
. The two curves intersect at
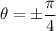 , so that
, so that
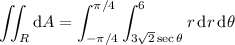
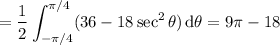
so again the total area would be
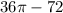 .
.
Or you can omit using calculus altogether and rely on some basic geometric facts. The region
 is a circular segment subtended by a central angle of
is a circular segment subtended by a central angle of
 radians. Then its area is
radians. Then its area is
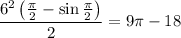
so the total area is, once again,
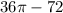 .
.
An even simpler way is to subtract the area of the square from the area of the circle.