Question

Find the value of k so that the line through points (-3, 2k) and (k,6) has a slope of 4

Answer 1

-1

Explanation:

To find the slope, I'm going to line up the points and subtract.

I will then put 2nd difference over first difference.

( -3 , 2k)

-( k , 6)

-----------------

-3-k , 2k-6

So the slope in terms of k is:

`(2k-6)/(-3-k)`.

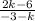We are also given the slope is 4 or 4/1.

This means we have the following equation to solve for k such that the slope is 4:

`(2k-6)/(-3-k)=(4)/(1)`

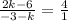
Cross multiply:

`1(2k-6)=4(-3-k)`

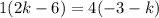
Distribute:

`2k-6=-12-4k`

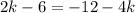
Add 4k on both sides:

`6k-6=-12`

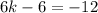
Add 6 on both sides:

`6k=-6`

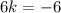
Divide both sides by 6:

`k=-1`

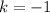
So k has to have a value of -1 for the slope to be 4.

Let's check:

(-3,-2)

(-1,6)

--------Subtracting

-2,-8

So -8/-2 is 4.

The check is good and the value for k as -1 as been verified.