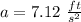Answer:
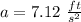
Step-by-step explanation:
For this exercise we need to use th following formula:
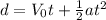
Where
 is the distance,
is the distance,
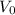 is the initial velocity,
is the initial velocity,
 is the acceleration and
is the acceleration and
 is the time.
is the time.
The first step is to convert from
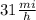 to
to
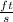 . Since:
. Since:
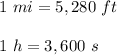
We get:
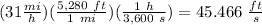
Knowing that:
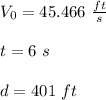
We can substitute values into the formula and solve for "a":
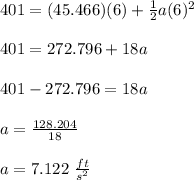
Rounded to the nearest 100th place: