Question

5x squared plus 13x-6=0​

Answer 1

Explanation:

The easiest way to solve this (in my opinion) is to use the Pythagorean theorem
`(-b+-√(b^2-4(a)(c)) )/(2a)`

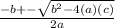
In this case, 5 is a, with the highest power, 13 is b, with the second highest power, and -6 is c, with a 0 power.

Or, looking at this equation
`ax^2+bx+c` we can gain that knowledge as well.

So let's plug these values in and solve!

`(-b+-√(b^2-4(a)(c)) )/(2a) = (-13+-√(13^2-4(5)(-6)) )/(2(5))\\=(-13+-√(169+120) )/(10)=(-13+-√(289) )/(10)=(-13+-17 )/(10)`

Now we simplify this into two different answers, one when we add, and one when we subtract:

`add:(-13+17 )/(10)=(4)/(10)=(2)/(5)\\subtract:(-13-17 )/(10)=(-30 )/(10)=-3`

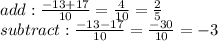
So, assuming the question asked to solve for x (which I'm assuming it did), our answers are x = -3 and
`(2)/(5)`

Answer:

x = -3

x =
`(2)/(5)`

Answer 2

Use the quadratic equation: you get values of x=2/5 and x=-3