Question

For what values of x is x2-36=5x true?

-9 and -4
-4 and 9
4 and -9
9 and 4

Answer 1

Its B. -4 and 9

Explanation:

Just took it and got 100%

Answer 2

Answer: SECOND OPTION

Explanation:

Given the following equation:

`x^2-36=5x`

You can follow these steps in order to find the values of "x" that makes the equation true:

1. Subtract
`5x` from both sides of the equation:

`x^2-36-5x=5x-5x\\\\x^2-5x-36=0`

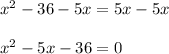
2. Factor the equation. Find two numbers whose sum be -5 and whose product be -36. These are 4 and -9:

`(x+4)(x-9)=0`

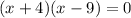
Then you get:

`x_1=-4\\\\x_2=9`

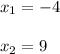
Checking:

`(-4)^2-36=5(-4)\\\\-20=-20`

TRUE

`(9)^2-36=5(9)\\\\45=45`

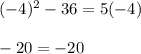
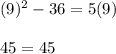
TRUE