Answer:
The mid-point (p + q , q + p) of AB is the same distance from the x-axis and the y-axis
Explanation:
* Lets explain how to solve the problem
- Any point will be equidistant from the x-axis and the y-axis must have
equal coordinates
- Ex: point (4 , 4) is the same distance from the x-axis and the y-axis
because the distance from the x-axis to the point is 4 (y-coordinate)
and the distance from the y-axis and the point is 4 (x-coordinate)
- If (x , y) is the mid-point of a segment its endpoints are
 and
and
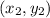 , then
, then
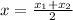 and
and
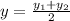
* Lets solve the problem
∵ Point A has coordinates (p , q)
∵ Point B has coordinates (p + 2q , q + 2p)
- The mid-point of AB is (x , y)
∵
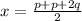
∴
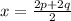
- Take 2 as a common factor from the terms of the numerator
∴

- Divide up and down by 2
∴ x = p + q
∵
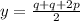
∴
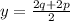
- Take 2 as a common factor from the terms of the numerator
∴
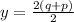
- Divide up and down by 2
∴ y = q + p
∴ The mid point of AB is (p + q , q + p)
- p + q is the same with q + p
∵ The x-coordinate of the mid point of AB is p + q
∵ The y-coordinate of the mid point of AB is q + p
∵ p + q = q + p
∴ The coordinates of the mid-point of AB are equal
- According the explanation above
∴ The mid-point (p + q , q + p) of AB is the same distance from the
x-axis and the y-axis