Question

An engineer in a locomotive sees a car stuck on the track at a railroad crossing in front of the train. When the engineer first sees the car, the locomotive is 330 m from the crossing and its speed is 25 m/s. If the engineer’s reaction time is 0.29 s, what should be the magnitude of the minimum deceleration to avoid an accident? Answer in units of m/s 2

Answer 1

Step-by-step explanation:

First, since the engineer is a slowpoke and he reacts a third of a second too late, the train will have 330 - 0.29*25 = 322,75 meters to stop. now, be
`x` (with
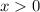`x>0`) the deceleration value for which the train bumps at the car and stops, you have two conditions:

`\left \{ {{25t-\frac12xt^2 = 322.75} \atop {0=25-xt}} \right.`

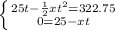
First states how much space the train has to stop, and the second tetermines how fast it slows down.

Solving the second for t, substituting in the first, and solving for x gives you a value of approximately
`1.94 m/s^2`.

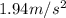As usual, double check the calculations for yourself, it's always a good practice