Question

Choose the equation that represents a line that passes through points (-6,4) and (2,0).

A) x+2y= 2
B) 2x-y= -16
C) x+2y= -8
D) 2x+y= 4

Please give a detailed explanation on how you solved the problem.

Answer 1

A.

Step-by-step explanation:

Just plug in the points to each equation.

A. x + 2y = 2

Plugging in (-6,4) (-6) + 2(4) = 2 ---> -6 + 8 = 2

Plugging in (2,0) (2) + 2(0) = 2 ---> 2 + 0 = 2

B. 2x + y = -16

Plugging in (-6.4) 2(-6) + (4) = -16 ---> -12 + 4 = -16 --> -8
`\\eq -16`

Because the first point didn't work there is no need to check the second one.

C. x + 2y = -8

Plugging in (-6,4) (-6) + 2(4) = -8 ---> -6 + 8 = -8 --> 2
`\\eq -8`

Again, because the first point didn't work there is no need to chek the next.

D. 2x + y = 4

Plugging in (-6,4) 2(-6) + (4) = 4 ---> -12 + 4 = 4 --> -8
`\\eq 4`

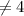
Even though the answer was A. you should still check each on of them because there can always be a mistake in your work.

Answer 2

A

Step-by-step explanation:

To find the equation of a line, the first thing that must be determined is the lines gradient. This can be determined by using the formula:

m = (Δy) / (Δx)

m = (4-0) / (-6-2)

m = 4 / -8

m = -0.5

The gradient has been determined, now we determine the y-intercept by using a point it passes through (either point cant be used because the line will pass through bother coordinates given)

y = mx + c (Using the point (2,0))

0 = (-0.5)(2) + c

c = 1

Since we have the y-intercept, a formula can be created for the line, and rearranging it, we can then find the correct option.

y = mx + c

y = (-0.5)x + 1

2y = -x + 2

x + 2y = 2