Question

Find the root using bisection method with initials 1 and 2 for function 0.005(e^(2x))cos(x) in matlab and error 1e-10?

Answer 1

The root is:

`c=1.5708`

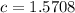
Step-by-step explanation:

Use this script in Matlab:

-------------------------------------------------------------------------------------

function [c, err, yc] = bisect (f, a, b, delta)

% f the function introduce as n anonymous function

% - a y b are the initial and the final value respectively

% - delta is the tolerance or error.

% - c is the root

% - yc = f(c)

% - err is the stimated error for c

ya = feval(f, a);

yb = feval(f, b);

if ya*yb > 0, return, end

max1 = 1 + round((log(b-a) - log(delta)) / log(2));

for k = 1:max1

c = (a + b) / 2;

yc = feval(f, c);

if yc == 0

a = c;

b = c;

elseif yb*yc > 0

b = c;

yb = yc;

else

a = c;

ya = yc;

end

if b-a < delta, break, end

end

c = (a + b) / 2;

err = abs(b - a);

yc = feval(f, c);

-------------------------------------------------------------------------------------

Enter the function in matlab like this:

f= @(x) 0.005*(exp(2*x)*cos(x))

You should get this result:

f =

function_handle with value:

@(x)0.005*(exp(2*x)*cos(x))

Now run the code like this:

[c, err, yc] = bisect (f, 1, 2, 1e-10)

You should get this result:

c =

1.5708

err =

5.8208e-11

yc =

-3.0708e-12

In addition, you can use the plot function to verify your results:

fplot(f,[1,2])

grid on