Question

Solve for x: x² - 14x + 49/x² - 49 = 3/17​

Answer 1

x = 10

Explanation:

Begin by factorising the numerator/ denominator of the left side

x² - 14x + 49 = (x - 7)² ← perfect square

x² - 49 = (x - 7)(x + 7) ← difference of squares

Thus left side becomes

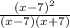`((x-7)^2)/((x-7)(x+7))` → x ≠ ± 7

Cancel (x - 7) on numerator/denominator, leaving

`(x-7)/(x+7)`

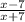
Returning to the equation, that is

`(x-7)/(x+7)` =
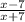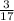`(3)/(17)` ( cross- multiply )

17(x - 7) = 3(x + 7) ← distribute both sides

17x - 119 = 3x + 21 ( subtract 3x from both sides )

14x - 119 = 21 ( add 119 to both sides )

14x = 140 ( divide both sides by 14 )

x = 10