Question

How much more would you earn in the first investment than in the second investment? $22,000 invested for 40 years at 14% compounded annually $22,000 invested for 40 years at 7% compounded annually You would earn $ more on the first investment than in the second investment

Answer 1

You would $3,825,999 more on the first investment than in the second investment

Explanation:

This is a compound interest problem.

The compond interest formula is given by:

`A = P(1 + (r)/(n))^(nt)`

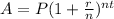
In which A is the amount of money, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per unit t and t is the time the money is invested or borrowed for.

The first investment:

A: our earnings, what we have to find

P = initial investment = 22,000

r = 0.14

n = 1

t = 40

`A = P(1 + (r)/(n))^(nt) = 22,000(1+(0.14)/(1))^(40) = $4,155,437.30`

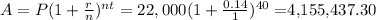
In the first investment, you would earn $4,155,437.30

The second investment:

A: our earnings, what we have to find

P = initial investment = 22,000

r = 0.07

n = 1

t = 40

`A = P(1 + (r)/(n))^(nt) = 22,000(1+(0.07)/(1))^(40) = $329,438.07`

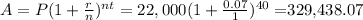
In the second investment, you would earn $329,438.07.

The difference

4,155,437.30 - 329,438.07 = $3,825,999.

You would $3,825,999 more on the first investment than in the second investment