Answer:
The following system is not linear.
The following system is time-invariant
Explanation:
To determine whether a system is linear, the following condition must be satisfied:
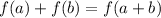
For
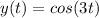 , we have
, we have
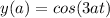
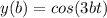
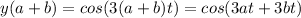
In trigonometry, we have that:
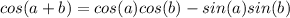
So
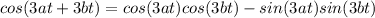

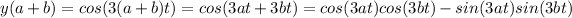
Since
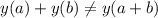 , the system
, the system
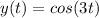 is not linear.
is not linear.
If the signal is not multiplied by time, it is time-invariant. So
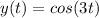 . Now, for example, if we had
. Now, for example, if we had
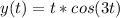 it would not be time invariant.
it would not be time invariant.