Answer:
The EMV of this project is -17,500
Explanation:
The EMV of the project is the Expected Money Value of the Project.
This value is given by the sum of each expected earning/cost multiplied by each probability.
So, in our problem
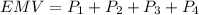
The problem states that there is a 25% chance of Snowmaggedon which will delay the project at a cost of $35,000. Since this is a cost,
 is negative.
is negative.
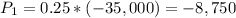
There is a 10% chance of cost of construction materials dropping saving the project $70,000. A saving is an earning, so
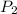 is positive
is positive
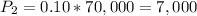
There is a 10% probability a labor strike will occur delaying the schedule with a cost of $40,000.
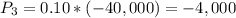
There is a 80% chance of new regulations mandated calling for higher inspection standards which will cost an additional $15,000 to mitigate
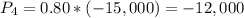
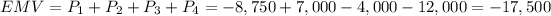
The EMV of this project is -17,500