Question

5. (6 marks) Use mathematical induction to prove that for each integer n ≥ 4, 5^n ≥ 2^2n+1 + 100.

(please take +100 into considersation since previous solution didnt )

Answer 1

Explanation:

We will prove by mathematical induction that, for every natural
`n\geq 4`,

`5^n\geq 2^(2n+1)+100`

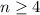We will prove our base case, when n=4, to be true.

Base case:

`5^4=625\geq 612=2^(2*4+1)+100`

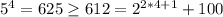
Inductive hypothesis:

Given a natural
`n\geq 4`,

`5^n\geq 2^(2n+1)+100`

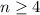Now, we will assume the induction hypothesis and then use this assumption, involving n, to prove the statement for n + 1.

Inductive step:

`2^(2(n+1)+1)+100=2^(2n+1+2)+100=\\=4*2^(2n+1)+100\leq 4(2^(2n+1)+100)\leq 4*5^n<5^(n+1)`

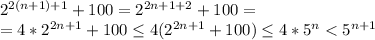
With this we have proved our statement to be true for n+1.

In conlusion, for every natural
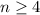`n\geq4`.

`5^n\geq 2^(2n+1)+100`