Answer:
The EMV of the project is $25,500.
Explanation:
The EMV of the project is the Expected Money Value of the Project.
This value is given by the sum of each expected earning multiplied by each probability
So, in our problem

The problem states that the project has a 60% of super success earning $50,000. So
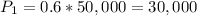
The project has a 15% chance of mediocre success earning $20,000. So
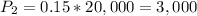
The project has a 25% probability of failure losing $30,000. So
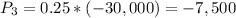
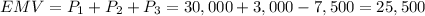
The EMV of the project is $40,500.