Answer:
The solution for this system is
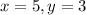 .
.
Explanation:
The Gauss-Jordan elimination method is done by transforming the system's augmented matrix into reduced row-echelon form by means of row operations.
We have the following system:
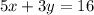

This system has the following augmented matrix.
![\left[\begin{array}{ccc}5&3&16\\-2&1&-13\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/6v1tys7sg237i4xe5ntgj16vyjokq9vwdy.png)
The first step is dividing the first line by 5. So:
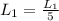
We now have
![\left[\begin{array}{ccc}1&(3)/(5)&(16)/(5)\\-2&1&-13\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/4go8hfxsj25pz5qybi3713kk2ae3ypjpkn.png)
Now i want to reduce the first row, so I do:
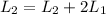
So we have
![\left[\begin{array}{ccc}1&(3)/(5)&(16)/(5)\\0&(11)/(5)&-(33)/(5)\end{array}\right][\tex].</p><p>Now, the first step to reduce the second row is:</p><p>[tex]L_(2) = (5L_(2))/(11)](https://img.qammunity.org/2020/formulas/mathematics/college/loba5z3bfcha5kr555athylogn8c55erdt.png)
So we have:
![\left[\begin{array}{ccc}1&(3)/(5)&(16)/(5)\\0&1&-3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/m6uvfqh15cn7ezyrp54c5wlbuxaeweh6i1.png) .
.
Now, to reduce the second row, we do:
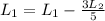
And the augmented matrix is:
![\left[\begin{array}{ccc}1&0&5\\0&1&-3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/4bt98rehfxdap9mhptfigwr4hg2m1ibfg1.png)
The solution for this system is
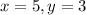 .
.