Question

A non conducting sphere of radius 0.04 m has a charge of 5.0 × 10^-9 C deposited on it. CalculateThe magnitude of the electric field at 0.02m from the center of the sphere

Answer 1

The electric field at a distance r = 0.02 m is 14062.5 N/C.

Solution:

Refer to fig 1.

As per the question:

Radius of sphere, R = 0.04 m

Charge, Q =
`5.0* 10^(- 9) C`

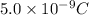
Distance from the center at which electric field is to be calculated, r = 0.02 m

Now,

According to Gauss' law:

`E.dx = (Q_(enclosed))/(\epsilon_(o))`

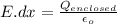
Now, the charge enclosed at a distance r is given by volume charge density:

`\rho = (Q_(enclosed))/(area)`

`\rho = (Q_(enclosed))/((4)/(3)\pi R^(3))`

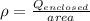
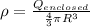
Also, the charge enclosed Q' at a distance r is given by volume charge density:

`\rho = (Q'_(enclosed))/((4)/(3)\pi r^(3))`

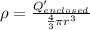
Since, the sphere is no-conducting, Volume charge density will be constant:

Thus

`(Q_(enclosed))/((4)/(3)\pi R^(3)) = (Q'_(enclosed))/((4)/(3)\pi r^(3))`

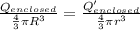
Thus charge enclosed at r:

Now, By using Gauss' Law, Electric field at r is given by:

`4\pi r^(2)E = (Q_(enclosed)r^(3))/(\epsilon_(o)R^(3))`

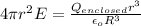
Thus

`E = (Q_(enclosed)r)/(4\pi\epsilon_(o)R^(3))`

`E = ((9* 10^(9))* 5.0* 10^(- 9)* 0.02)/(0.04^(3))`

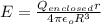
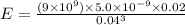
E = 14062.5 N/C