Question

A wheel initially spinning at wo = 50.0 rad/s comes to a halt in 20.0 seconds. Determine the constant angular acceleration and the number of revolutions it makes before stopping. An athlete is holding a 2.5 meter pole by one end. The pole makes an angle of 60 with the horizontal. The mass of the pole is 4 kg. Determine the torque exerted by the pole on the athlete's hand. (The mass of the pole can be assumed to be concentrated at the center of mass.)

Answer 1

(I). The angular acceleration and number of revolution are -2.5 rad/s² and 500 rad.

(II). The torque is 84.87 N-m.

Step-by-step explanation:

Given that,

Initial spinning = 50.0 rad/s

Time = 20.0

Distance = 2.5 m

Mass of pole = 4 kg

Angle = 60°

We need to calculate the angular acceleration

Using formula of angular velocity

`\omega=-\alpha t`

`\alpha=-(\omega)/(t)`

`\alpha=-(50.0)/(20.0)`

`\alpha=-2.5\ rad/s^2`

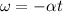
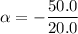
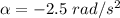
The angular acceleration is -2.5 rad/s²

We need to calculate the number of revolution

Using angular equation of motion

`\theta=\omega_(0)t+(1)/(2)\alpha t`

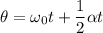
Put the value into the formula

`\theta=50*20-(1)/(2)*2.5*20^2`

`\theta=500\ rad`

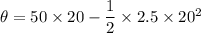
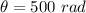
The number of revolution is 500 rad.

(II). We need to calculate the torque

Using formula of torque

`\vec{\tau}=\vec{r}*\vec{f}`

`\tau=r* f\sin\theta`

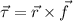
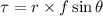
Put the value into the formula

`\tau=2.5*4* 9.8\sin60`

`\tau=84.87\ N-m`

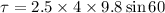
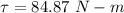
Hence, (I). The angular acceleration and number of revolution are -2.5 rad/s² and 500 rad.

(II). The torque is 84.87 N-m.