Answer:
The answer is very close to
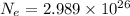 , where
, where
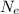 is the number of electrons.
is the number of electrons.
Step-by-step explanation:
First we take into account that the block weighs 1Kg, and that the number of protons and electrons is the same. As the electron mass is tiny even compared to that of the proton and neutrons we can neglect it in our considerations.
Let's start by equating the mass of all protons and neutrons to the mass of the of the object:

Where
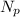 and
and
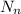 is the number of protons and neutrons respectively.
is the number of protons and neutrons respectively.
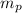 and
and
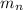 is the mass of an proton and a neutron respectively. Because the number of protons and neutrons is equal we can say the following
is the mass of an proton and a neutron respectively. Because the number of protons and neutrons is equal we can say the following
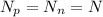 , thus we have:
, thus we have:

On the other hand we have that the sum of all charges is less than the absolute value of 1C, we can express this by the following:
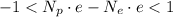
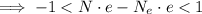
Where
 is the proton charge (same as for the electron). We continue with the inequality:
is the proton charge (same as for the electron). We continue with the inequality:
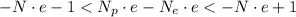

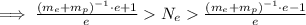
We have the estimated number of electrons bound. Because
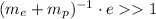 We can neglect the ones on the rightmost and leftmost parts of the inequality. We then have
We can neglect the ones on the rightmost and leftmost parts of the inequality. We then have
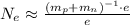
Using the table values of the mass of the proton, mass of the neutron and the electron charge e we get
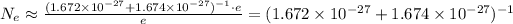
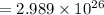 electrons
electrons