Question

Use mathematical induction to prove that for each integer n ≥ 4, 5^n ≥ 2^2n+1 + 100. (it is 5 to power of n and 2 to the power of 2n+1)

Answer 1

Explanation:

The statement to be proved using mathematical induction is:

1. "For every
   `n\geq 4`,
   `5^n\geq 2^(2n+1)+100`

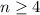We will begin the proof showing that the base case is satisfied (n=4).

`5^4=625\geq 612=2^(2*4+1)+100`.

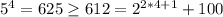Then, 1 is true for n=4.

Now we will assume that the statement holds for some arbitrary natural number
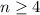`n\geq 4` and prove that then, the statement holds for n+1. Observe that

`2^(2(n+1)+1)+100=2^(2n+1+2)+100=4*2^(2n+1)+100\leq 4(2^(2n+1)+100)\leq 4*5^n<5^(n+1)`

With this the inductive step has been proven and then, our statement is true,

For every
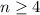`n\geq 4`,
`5^n\geq 2^(2n+1)+100`