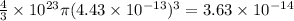Answer:
(a)
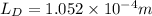
N =
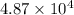
(b)
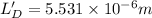
N' =

(c)
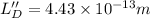
N'' =
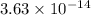
Solution:
As per the question, we have to calculate the Debye,
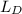 length and N for the given cases.
length and N for the given cases.
Also, we utilize the two relations:
1.
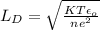
2. N =
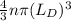
Now,
(a) n =
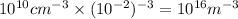
KT = 2 eV
Then
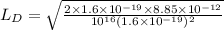
(Since,
e =
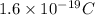
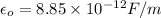 )
)
Thus
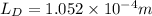
Now,
N =
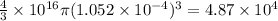
(b) n =
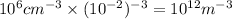
KT = 0.1 eV
Then
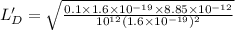
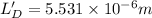
N' =
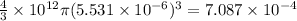
(c) n =
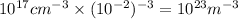
KT = 800 eV
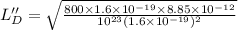
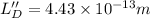
N'' =